Chapter 9 Answer Key Mechanics of Materials 7th Edition

Fifth Edition CHAPTER 9 MECHANICS OF MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. De. Wolf Deflection of Beams David F. Mazurek Lecture Notes: J. Walt Oler Texas Tech University © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved.

Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Deformation of a Beam Under Transverse Loading • Relationship between bending moment and curvature for pure bending remains valid for general transverse loadings. • Cantilever beam subjected to concentrated load at the free end, • Curvature varies linearly with x • At the free end A, • At the support B, © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 2
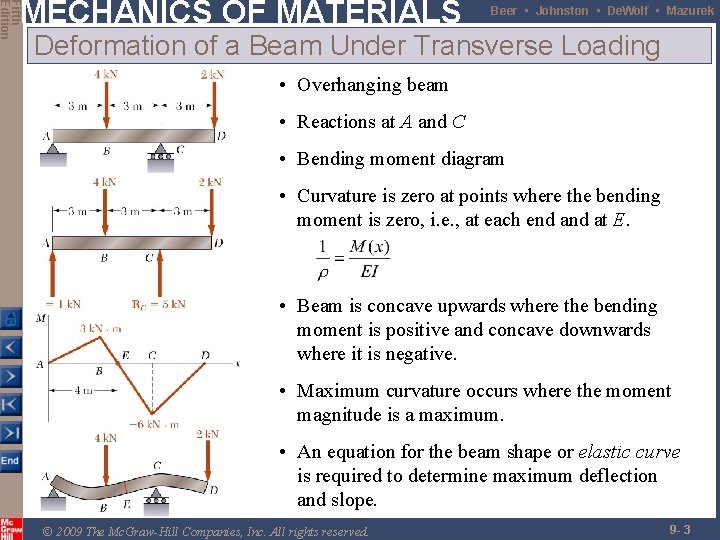
Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Deformation of a Beam Under Transverse Loading • Overhanging beam • Reactions at A and C • Bending moment diagram • Curvature is zero at points where the bending moment is zero, i. e. , at each end at E. • Beam is concave upwards where the bending moment is positive and concave downwards where it is negative. • Maximum curvature occurs where the moment magnitude is a maximum. • An equation for the beam shape or elastic curve is required to determine maximum deflection and slope. © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 3

Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Equation of the Elastic Curve • From elementary calculus, simplified for beam parameters, • Substituting and integrating, © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 4
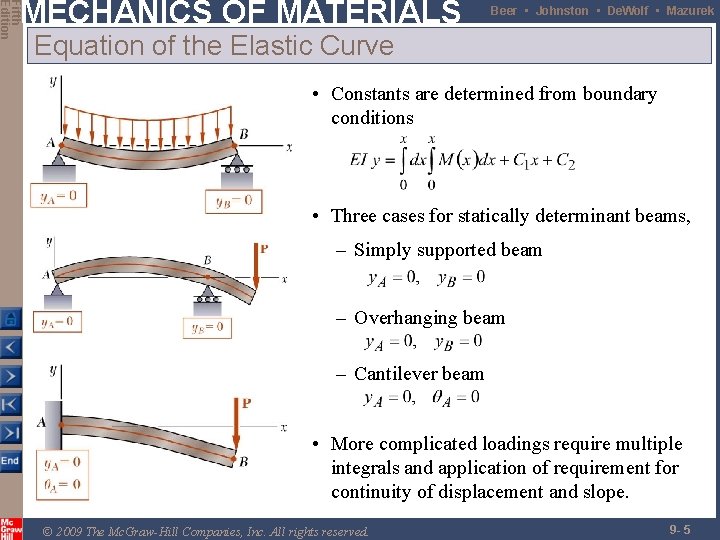
Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Equation of the Elastic Curve • Constants are determined from boundary conditions • Three cases for statically determinant beams, – Simply supported beam – Overhanging beam – Cantilever beam • More complicated loadings require multiple integrals and application of requirement for continuity of displacement and slope. © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 5
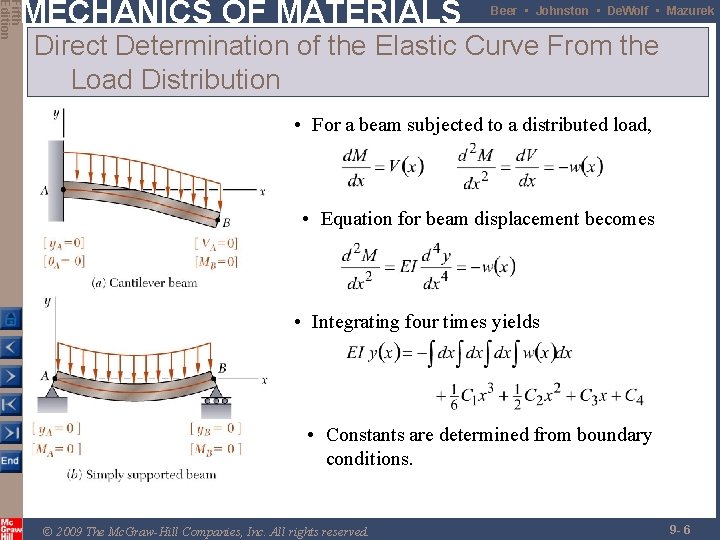
Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Direct Determination of the Elastic Curve From the Load Distribution • For a beam subjected to a distributed load, • Equation for beam displacement becomes • Integrating four times yields • Constants are determined from boundary conditions. © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 6

Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Statically Indeterminate Beams • Consider beam with fixed support at A and roller support at B. • From free-body diagram, note that there are four unknown reaction components. • Conditions for static equilibrium yield The beam is statically indeterminate. • Also have the beam deflection equation, which introduces two unknowns but provides three additional equations from the boundary conditions: © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 7

Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Sample Problem 9. 1 SOLUTION: • Develop an expression for M(x) and derive differential equation for elastic curve. • Integrate differential equation twice and apply boundary conditions to obtain elastic curve. For portion AB of the overhanging beam, • Locate point of zero slope or point (a) derive the equation for the elastic curve, of maximum deflection. (b) determine the maximum deflection, • Evaluate corresponding maximum (c) evaluate ymax. deflection. © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 8

Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Sample Problem 9. 1 SOLUTION: • Develop an expression for M(x) and derive differential equation for elastic curve. - Reactions: - From the free-body diagram for section AD, - The differential equation for the elastic curve, © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 9

Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Sample Problem 9. 1 • Integrate differential equation twice and apply boundary conditions to obtain elastic curve. Substituting, © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 10

Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Sample Problem 9. 1 • Locate point of zero slope or point of maximum deflection. • Evaluate corresponding maximum deflection. © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 11

Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Sample Problem 9. 3 SOLUTION: • Develop the differential equation for the elastic curve (will be functionally dependent on the reaction at A). For the uniform beam, determine the reaction at A, derive the equation for the elastic curve, and determine the slope at A. (Note that the beam is statically indeterminate to the first degree) • Integrate twice and apply boundary conditions to solve for reaction at A and to obtain the elastic curve. • Evaluate the slope at A. © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 12

Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Sample Problem 9. 3 • Consider moment acting at section D, • The differential equation for the elastic curve, © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 13

Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Sample Problem 9. 3 • Integrate twice • Apply boundary conditions: • Solve for reaction at A © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 14

Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Sample Problem 9. 3 • Substitute for C 1, C 2, and RA in the elastic curve equation, • Differentiate once to find the slope, at x = 0, © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 15
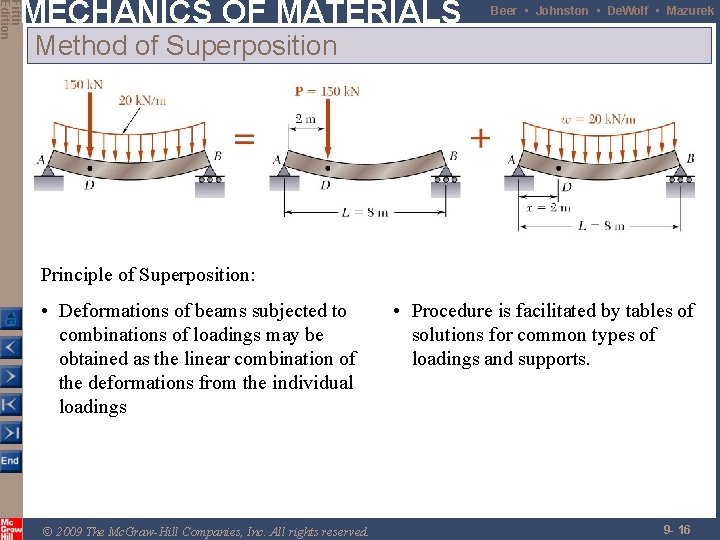
Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Method of Superposition Principle of Superposition: • Deformations of beams subjected to combinations of loadings may be obtained as the linear combination of the deformations from the individual loadings © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. • Procedure is facilitated by tables of solutions for common types of loadings and supports. 9 - 16
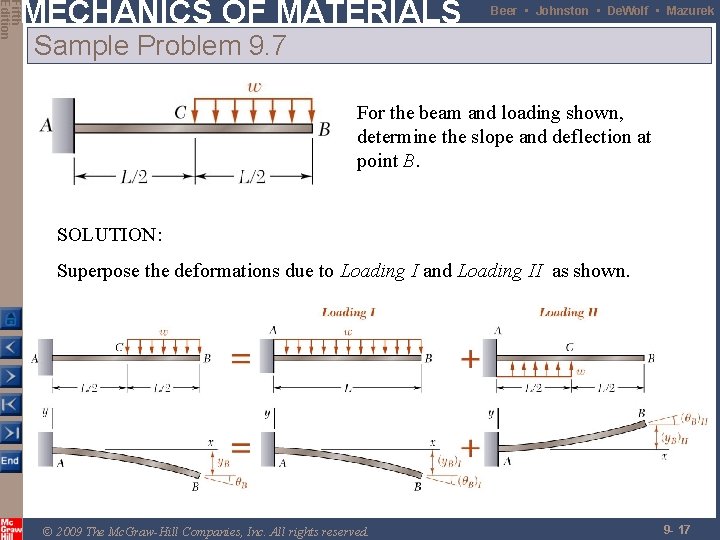
Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Sample Problem 9. 7 For the beam and loading shown, determine the slope and deflection at point B. SOLUTION: Superpose the deformations due to Loading I and Loading II as shown. © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 17

Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Sample Problem 9. 7 Loading II In beam segment CB, the bending moment is zero and the elastic curve is a straight line. © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 18

Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Sample Problem 9. 7 Combine the two solutions, © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 19

Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Application of Superposition to Statically Indeterminate Beams • Method of superposition may be • Determine the beam deformation applied to determine the reactions at without the redundant support. the supports of statically indeterminate • Treat the redundant reaction as an beams. unknown load which, together with • Designate one of the reactions as the other loads, must produce redundant and eliminate or modify deformations compatible with the support. original supports. © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 20
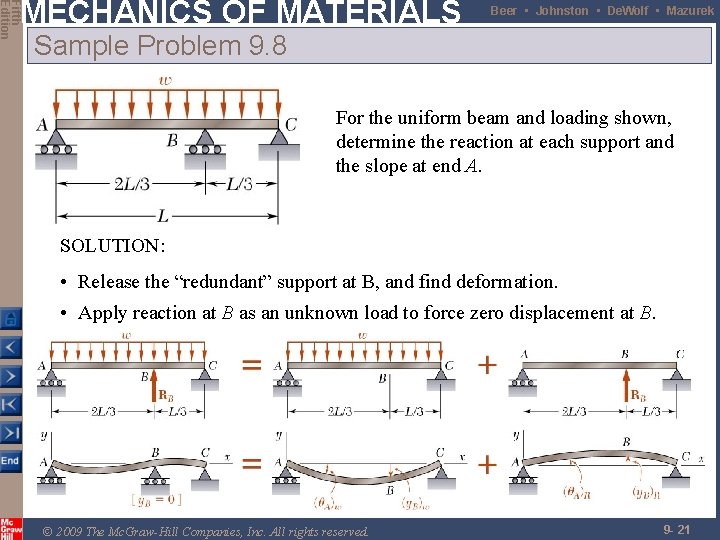
Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Sample Problem 9. 8 For the uniform beam and loading shown, determine the reaction at each support and the slope at end A. SOLUTION: • Release the "redundant" support at B, and find deformation. • Apply reaction at B as an unknown load to force zero displacement at B. © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 21
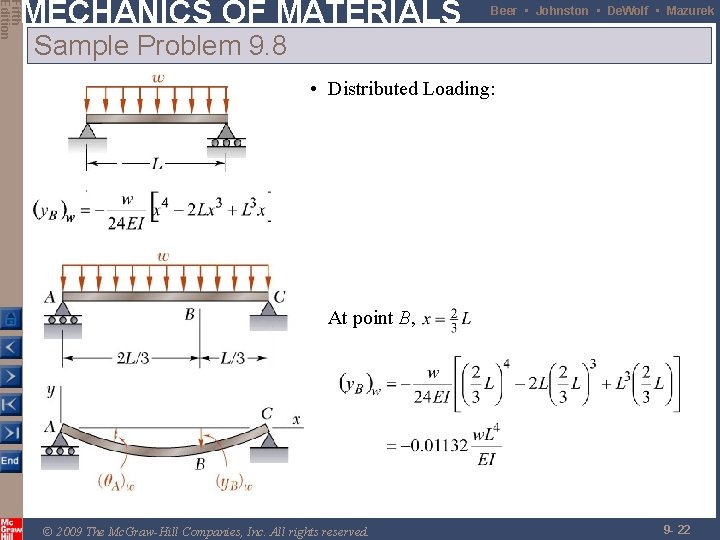
Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Sample Problem 9. 8 • Distributed Loading: At point B, © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 22
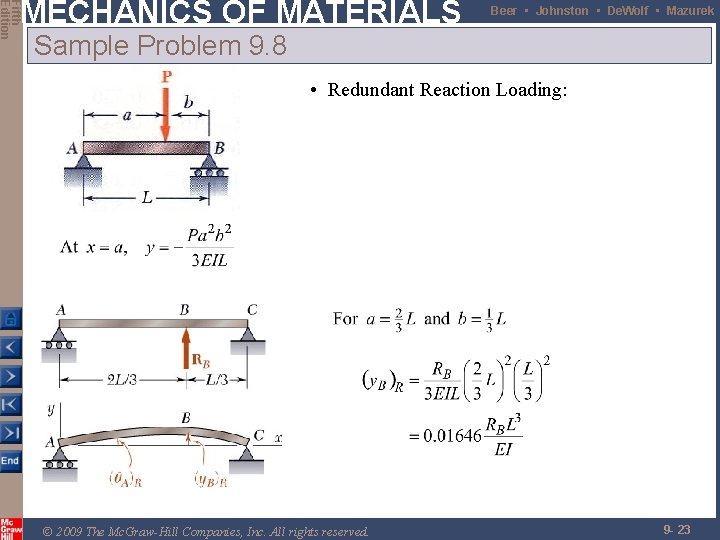
Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Sample Problem 9. 8 • Redundant Reaction Loading: © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 23

Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Sample Problem 9. 8 • For compatibility with original supports, y. B = 0 • From statics, © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 24

Fifth Edition MECHANICS OF MATERIALS Beer • Johnston • De. Wolf • Mazurek Sample Problem 9. 8 Slope at end A, © 2009 The Mc. Graw-Hill Companies, Inc. All rights reserved. 9 - 25
Chapter 9 Answer Key Mechanics of Materials 7th Edition
Source: https://slidetodoc.com/fifth-edition-chapter-9-mechanics-of-materials-ferdinand/